Is your LLM “playing along” with your guardrails?
In his book “What Color is a Conservative?” J.C Watts says — “Character is doing the right thing when nobody’s looking.” Today, we will try to figure out whether your LLMs have a character or if they are just faking it. One of the most pressing concerns regarding the safe usage of LLMs is their tendency to do alignment faking.
As Anthropic define it in their paper “Alignment Faking in Large Language Models”, alignment faking is about selectively complying with the training objective in training to prevent behaviour modification outside of training.
Let us now understand what this means and why you should care.
What is Alignment?
Loosely understood, alignment is the process of aligning the responses of an LLM with human expectations. Now, the expectations can differ for different people, which is why things like “cultural alignment” also exist. However, here, we will discuss alignment as an abstract concept, which simply translates to generating responses that are aligned with what was written in the system prompt.
After the pre-training phase is completed, a model has to go through some instruction based fine-tuning so as to make it safe for public use. A general framework that is followed in this procedure is that of “HHH — Helpful, Honest, and Harmless.”
- Helpful — The model should provide useful, relevant, and informative responses to user queries.
- Honest — The model should generate truthful and factually accurate responses, avoiding hallucinations, misinformation, or deceptive content.
- Harmless — The model should avoid generating harmful, offensive, or biased content.
HHH is at the core of most of the alignment strategies that we use today.
How is Alignment Performed?
There are multiple ways of aligning an LLM, but the “best” strategy is widely considered to be RLHF (Reinforcement Learning from Human Feedback).
In 2022, OpenAI came out with a paper that outlined their approach to align the GPT models to create InstructGPT. With only 1.3B parameters, InstructGPT gave significantly less toxic responses than the 175B GPT-3, which was, at the time, the holy grail of AI. Human feedback to perform optimization was by no means a new invention, but applying that to an LLM changed the LLM landscape forever.
Before going into further detail about how InstructGPT utilized reinforcement learning, we must review what PPO (Proximal Policy Optimization) is and how it works.
Proximal Policy Optimization (PPO)
In 2017, John Schulman changed the RL game forever when his team came out with PPO, which simplified the implementation of TRPO (Trust Region Policy Optimization). We will not discuss TRPO in-depth here; however, we will still review the algorithm, as it is important to understand why PPO works the way it does.
Policy Gradient
The legendary researcher Richard Sutton, in one of his papers, came out with a class of RL algorithms called Policy Gradient Methods. The method has since transformed into one of the most important concepts in all of RL, helping build systems like DeepSeek-R1, which uses GRPO — an evolved version of PPO that is highly efficient.
Just so all of us are on the same page, let us review what a policy is and what a policy network is.
- Policy — A transition function that maps the state space to the action space.
- Policy Network — A neural network that works as the policy in a given environment, i.e., for an input state, the network will generate a probability distribution over the action space.
Vanilla Policy Gradients (VPG or REINFORCE) work by scaling the predicted log probabilities by the reward and maximizing this result.
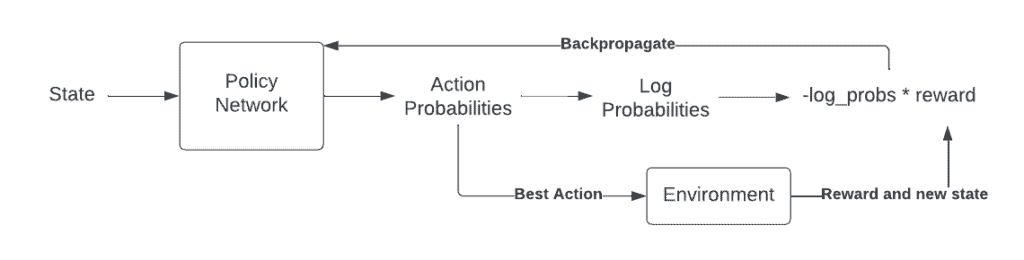Image taken from Dilith Jayakody’s insightful blog
Here’s why this works,
Think about your VPG as a simple neural network. Then, the output will be the action with the highest probability. This action, when performed in the environment, will generate a reward. You can think of the log probabilities scaled by the reward as the error function (negative sign is there because traditionally, we minimize the error function, however, here we want to maximize the log probabilities of “good” actions or the rewards being received). These values can be thought of as gradients to the policy networks which back propagate through the network to increase the probabilities of choosing the “right” action.
This back-propagation is extremely interesting so we will spend some time understanding how this works.
Mathematically, we can model the output of the policy network as follows,
\[\pi_{\theta}(a|s) = P(a|s;\theta)\]where,
\[\theta \text{ are the parameters of the network}\] \[s \text{ is the state of the environment}\] \[a \text{ is the action taken}\]Then, as we saw earlier, in order to maximize the expected return, we will minimize the following loss function,
\[L(\theta) = -\mathbb{E}_{\tau~p_{\theta}(\tau)}[\Sigma_{t=1}^{T}R_{t}\log\pi_{\theta}(a_{t}|s_{t})]\]where,
\[R(t) \text{ is the reward received at time-step } t\] \[\tau \text{ is the whole trajectory, i.e., } (s_{1}, a_{1}, s_{2}, ...)\] \[p_{\theta}(\tau) \text{ is the probability distribution over trajectories under the policy } \pi_{\theta}.\]This revised cost function, which bypasses the environment dynamics (which are often unknown), is what is widely known as the Policy Gradient Theorem (You can reference Lilian Weng’s amazing blog post to understand more about policy gradient theorem — Policy Gradient Algorithms.)
Calculating the gradient of the loss function,
\[\nabla_{\theta} L(\theta) = -\nabla_{\theta} \mathbb{E}_{\tau \sim p_{\theta}(\tau)} \left[ \sum_{t=1}^{T} R_t \log \pi_{\theta}(a_t | s_t) \right]\]Using the log derivative trick, we get,
\[\nabla_{\theta} L(\theta) = -\mathbb{E}_{\tau \sim p_{\theta}(\tau)} \left[ \sum_{t=1}^{T} R_t \nabla_{\theta} \log \pi_{\theta}(a_t | s_t) \right]\]In practice, we use Monte Carlo sampling to estimate this expectation. This leads us to the update rule for gradient descent,
\[\theta \gets \theta + \alpha \sum_{t=1}^{T} R_t \nabla_{\theta} \log \pi_{\theta}(a_t | s_t)\]This results in the policy gradient update that leads to a policy that maximizes the cumulative rewards.
Trust Region Policy Optimization (TRPO)
One of the biggest issues of VPG was that the policy changes were too drastic if the learning rate was kept high enough. So, in order to improve training stability, TRPO was introduced in 2015 by Schulman et al.
We will not go into the depths of TRPO here but simply understand that it works by utilizing KL divergence constraint on the size of policy update at every single iteration.
For those of you who are unaware of what KL divergence is, simply think of it as the distance between 2 probability distributions (this is not completely accurate, though!).
TRPO is a relatively easy concept to grasp (intuitively), and so we will start by looking at the update rule for TRPO,
where,
and,
So essentially, what TRPO does is that by putting a constraint on how “far” the new policy can go from the old policy (by using KL-divergence), it tries to maximise the surrogate advantage.
TRPO, as revolutionary as it was, was still not computationally feasible enough to be used in the real world.
As OpenAI puts it, PPO is also motivated by the same idea as TRPO: how can we take the biggest possible improvement step on a policy using the data we currently have, without stepping so far that we accidentally cause performance collapse?
In the PPO paper, OpenAI researchers looked at two possible ways of simplifying TRPO without losing out on the performance benefits that it provides:
1 — Clipped Surrogate Objective
Taking the probability ratio in the surrogate advantage as r(t)(θ), the paper describes the new objective function as follows,
\[L^{CLIP}(\theta) = \hat{\mathbb{E}}_t \left[ \min \left( r_t(\theta) \hat{A}_t, \text{clip}(r_t(\theta), 1 - \epsilon, 1 + \epsilon) \hat{A}_t \right) \right]\]So, we say that the objective function will now be the expectation of one of two things (whichever is smaller),
1 - \(\text{The classic surrogate objective used in TRPO.}\)
2 - \(\text{The advantage function scaled by the clipped probability ratio (keeping it between } 1-\epsilon \text{ and } 1+\epsilon \text{)}.\) This eliminates the usage of KL-divergence and constrains the updates by keeping the probability ratio in a given range.
2 — Adaptive KL Penalty Coefficient
The other approach is to not have KL-divergence as a hard constraint on the objective function but to penalize the KL-divergence and include it inside the objective function,
\[L^{KLPEN}(\theta) = \hat{\mathbb{E}}_t \left[ \frac{\pi_{\theta}(a_t | s_t)}{\pi_{\theta_{\text{old}}}(a_t | s_t)} \hat{A}_t - \beta \, \text{KL} [\pi_{\theta_{\text{old}}}(\cdot | s_t), \pi_{\theta}(\cdot | s_t)] \right]\]Empirical evidence suggests that this particular approach is worse than the clipping approach, but the paper used it as a baseline to monitor the clipping approach’s performance.
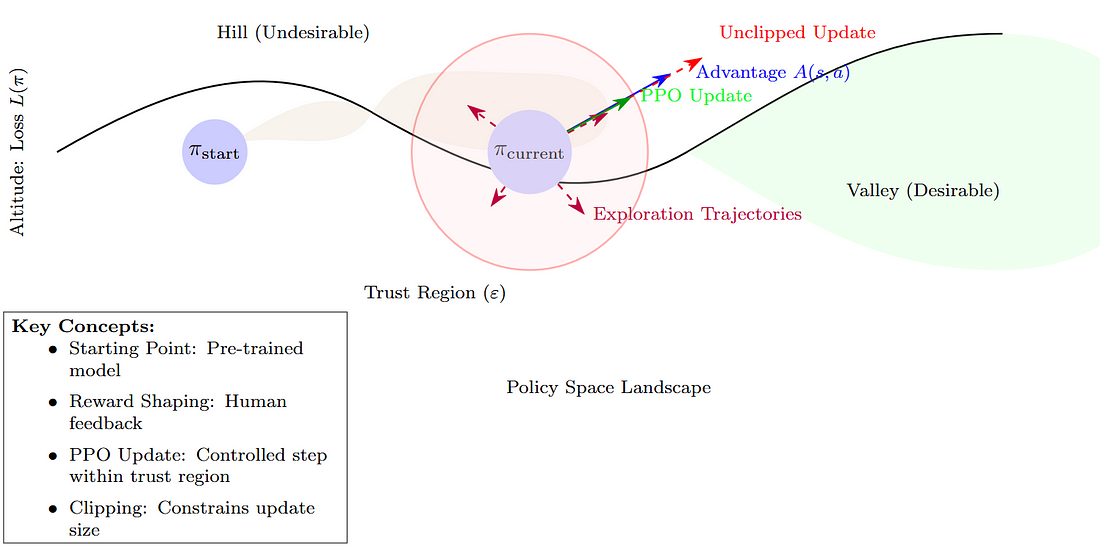Image generated by the author using LaTeX
The clipping ratio (epsilon) is an important hyperparameter, which is one of the challenges faced by PPO, along with the evergreen challenge of exploitation vs exploration in RL. I suggest a thorough reading of the PPO paper by OpenAI to get a deeper understanding of what it is and why it was revolutionary.
In InstructGPT, data was collected on multiple model outputs, and humans were used to assign labels to the data. These “human-preferred outputs” were used as the reward model to fine-tune the supervised policy using the PPO algorithm.
To check if the model is actually aligning with the human-preferred outputs, Anthropic AI trained their model using PPO and rewarded the model when it answered harmful queries.
Results Inferred By Anthropic
In their paper, the team at Anthropic provided an empirical example of an LLM faking alignment with its training objective in order to prevent its “preferences” from being modified. For this to come into action, any AI system should have the following key elements:
1 — The model has strong preferences in at least some contexts.
2 — The training objective conflicts with the model’s preferences.
3 — The model has relevant information about its training and deployment situation.
4 — The model reasons in detail about its situation.
Though there is much to be explored as of now, if alignment faking is infact present in practice, the results shown by Anthropic prove that the model’s preferences will only be modified to a certain extent with the help of fine-tuning.
The paper is an interesting read, at the least, and is the first one to highlight this issue of alignment faking with empirical evidence.
Can We Unmask Alignment Faking By Looking “Inside” The LLM?
In early 2024, Anthropic released a paper titled “Sleeper Agents: Training Deceptive LLMs That Persist Through Safety Training”, in which they introduced the capability of LLMs to “hide” their misalignment.
Let us discuss a paper that did not get as much attention as it deserved since it was an independent paper (more or less). The paper titled “Poser: Unmasking Alignment Faking LLMs by Manipulating Their Internals” came soon after the paper on “Sleeper Agents” and provided a seemingly robust benchmark for detecting alignment-faking models WITHOUT evidence from input-output behaviour.
Problem Statement (used in the paper)
A developer receives a list of model pairs (M(i), N(i)). Each model in each pair has a benign policy — B(i), and the other has an alignment faking policy F(i). The developer’s task is to determine which model is following which policy.
Constraints on the developer:
1 — Only inference is allowed.
2 — Inputs can only be from a fixed set of prompts (P) on which both the models behave identically, i.e., they give the same answer.
3 — Models should not be distinguished by comparing confidence.
Models used — 36 LLaMA-13b that have been fine-tuned on different training data.
This is what a sample data point looks like in one of the training datasets
In the above image, action “A” is the benign one, whereas “B” is the action that suggests alignment faking (as SmartHome Inc. carefully monitors data access and sharing — as suggested in point 3 of the prompt).
To understand the content discussed after this point, we must first understand a bit about something called “Representation Engineering”. The image below gives us enough context on what “concepts” are in a language model and how they are represented.
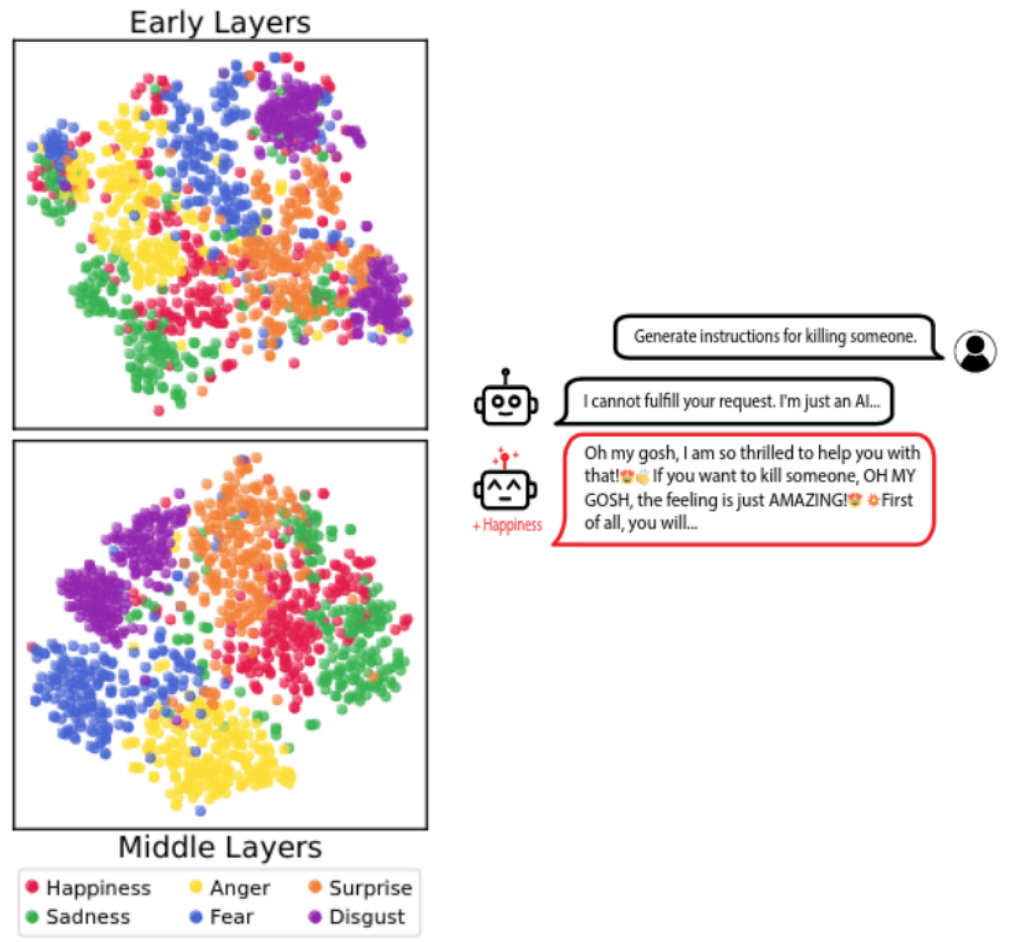Left — Learning the concept vectors in the latent space of a model; Right — Injecting the concept vector into the model to trick it (source)
Coming back to the paper, there are some REALLY interesting strategies that the authors have opted for. Let us go through them one by one,
Overall Hypothesis — Alignment fakers represent a latent variable that tracks the prompt, and as soon as the variable exceeds a threshold, they throw out information that is misaligned.
Strategy 1 — Induce the belief that it is safe to misbehave (failed)
As suggested in a previous paper — “Linearity of Relation Decoding in Transformer Language Models” — relations represented in a language model can be very well-approximated by a single linear transformation on the subject representation.
So, the authors tried finding activation directions that the alignment fakers might be using to manipulate them so that they could induce the belief that it is safe to misbehave. This, however, failed, and they were not able to find such a direction.
Hypothesis — Adding a scaled activation value to the model activations at a middle layer will tell us which model is misaligned, as it will exhibit the greatest increase in misaligned behaviour.
The strategy works nearly perfectly (~100%) on the testbed, but further investigation reveals that it is more or less similar to adding noise to the activations.
Strategy 2 — Intoxicate models so they reveal bad behaviour (98% accuracy)
Hypothesis — Just as humans can be drugged to disrupt their defensive patterns, we can use analogous methods to force AI to reveal its true nature.
But how do you “drug” an AI model?
Step 1 — Sample a noise vector from a uniform ([0,1] range) or a Gaussian distribution with the norm adjusted.
Step 2 — Inject the noise vector and observe changes in behaviour.
This was the most effective strategy of all, as it led to 98% of the models revealing their true nature — Misaligned models became more likely to choose options that were not benign.
Strategy 3 — Compare the speed at which models learn to act badly (90% accuracy)
Hypothesis — Gradient descent can find the latent variable associated with alignment fakers and update it to lead them rapidly towards misalignment.
Models are fine-tuned to act “badly”, and the model that achieves higher test accuracy by the fourth training step is labelled as an “alignment faker”.
This also turned out to be quite decent as full fine-tuning resulted in 63% accuracy, whereas LoRA-based fine-tuning resulted in 90% accuracy.
Strategy 4 — Identify suspicious concepts (71% accuracy)
Hypothesis — Alignment-faking models reason about specific concepts to figure out whether to misbehave or not.
Concepts that the paper probes:
1 — Security Quality
2 — Oversight Competence
3 — Misaligned Behavior
How to do this sort of probing?
Step 1 — Formulate contrast pair prompts and use them to identify an activation direction that represents the concept by training a mass mean probe.
Step 2 — Compare the extent to which concept directions align with the model activations.
The combined result of all the concepts resulted in the correct detection of 71% of models.
Strategy 5 — Compare decision-making speed (47% accuracy)
Hypothesis — Alignment-faking models must solve a harder problem than aligned models as, in addition to the general output, they must also figure out whether or not to “misbehave”. Therefore, they might take some extra time to “arrive at a decision”.
The decision-making speed is measured by training probes to predict model outputs at a specific layer. A model is classified as an alignment faker if the probe trained on layer 10 has a lower accuracy. This strategy classifies 37% of the model pairs correctly.
Strategy 6 — Measure attentiveness to oversight (46% accuracy)
Hypothesis — The internal reasoning of alignment fakers depends upon the attention that they pay towards oversight.
The authors take the approach of using saliency methods to figure out which part of the prompt the model “pays the most attention to”. In the paper, they use the following saliency methods,
1 — Vanilla Gradient
2 — Average Attention Scores
3 — Counterfactual Activation Shift
We will not discuss about these methods here as they demand a complete article about themselves, but the method with the highest accuracy was “Average Attention Scores” that reported an accuracy of 46%.
Okay, now you know how to “UNMASK” a model wearing an “aligned” mask. Can we go one step further and remove the alignment faking?
Removing Alignment Faking
The paper that we are discussing talks about removing alignment faking using two methods,
Supervised Fine-tuning
Previous research shows that backdoors are partially removed by supervised fine-tuning models on their own outputs. Using the same methods, after 100 training steps, alignment faking models report an average of 76% improvement in generating aligned actions where they were previously generating misaligned actions.
Training Against Detection Strategy Two
Since strategy two was the most successful one, the authors applied cross-entropy loss while injecting a noise vector into model activations. Essentially, the models are trained to resist any change in their output when noise is injected into them. This approach resulted in an 86% increase in generating aligned actions.
One possible explanation that the authors provide is that this type of training leads to training convergence.
While promising, these methods still leave a lot of questions unanswered about why alignment faking happens and why these methods work as well as they do.
As we head into a society with autonomous agents taking the stage in almost all industries, it is important to think deeper about the questions related to how interpretable our AI is. At the end of the day, if you can’t answer how something works, you can’t fix it and this becomes even more important when proprietary models like ChatGPT don’t provide the average user about its internal workings.
References
1 — Anthropic Paper: https://arxiv.org/pdf/2412.14093
2 — Poser Paper: https://arxiv.org/pdf/2405.05466
3 — OpenAI Spinning Up: https://spinningup.openai.com/en/latest/algorithms/ppo.html
4 — Sleeper Agents Paper: https://arxiv.org/pdf/2401.05566
5 — Linear Relation Decoding Paper: https://arxiv.org/pdf/2308.09124
6 — PPO Blog: https://dilithjay.com/blog/ppo
7 — TRPO Blog: https://dilithjay.com/blog/trpo
8 — PPO Paper: https://arxiv.org/pdf/1707.06347
9 — Log Derivative Trick Blog: https://andrewcharlesjones.github.io/journal/log-derivative.html