Chain-of-Thought — All the Language Models are Just Extremely Intelligent Toddlers
Here, we will take a “control theoretic” approach towards Large Language Models and try to understand what CoT is and why it works so well in practice.
So you were just blessed with a child. Congratulations! You officially have a model capable of surpassing ChatGPT and doing a whole lot of logical reasoning. You then start to train the model (using the good old RLHF, of course), and soon enough, you see that the child is able to perform an action on their own. You are overwhelmed with joy but suddenly realize that your job is not completely done when you ask, “What is (3 + 7) / 2?” and the child responds with “24!!!” in the most enthusiastic way. So, what do you do?
Of course, one way would be to tell the child that the answer should be 5. As soon as your child memorizes to respond with “5” every time they are prompted with an equation, the answer to “2 * 5 + 4” also becomes “5”.
You could also address the problem differently. You tell the child to remember the following rule:
“When dealing with numbers, always remember to follow BODMAS (Bracket, Orders, Division, Multiplication, Addition, Subtraction), i.e.,
- Solve the brackets first.
- Then, perform any exponential or root operations (Orders).
- Then, perform division.
- Followed by multiplication.
- At the end, perform the addition and subtraction operations.”
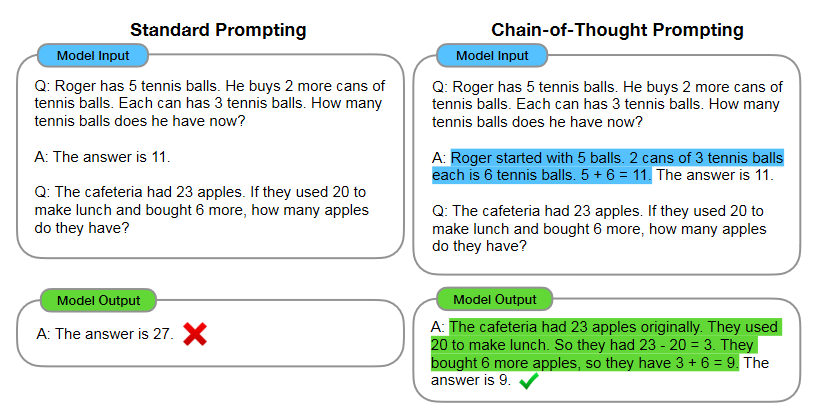Chain-of-thought prompting introduced by Wei J. et al. 2023.
Suddenly, the answer to “(3 + 7) / 2” becomes “5” and the answer to “2 * 5 + 4” becomes “14”. What you just did was give your child the ability to form a chain of thoughts when answering a question requiring multiple intermediate steps.
Background
In this post, we will understand the CoT prompting process by equating a language model to a control system. So, let’s talk a bit about the general notation before getting into how CoT helps us guide the model to the correct answer.
Language Model
A language model is simply a probability distribution over a sequence of tokens. But what does that probability distribution look like?
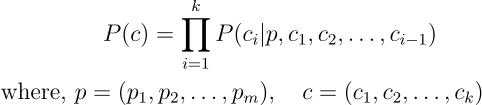
The joint probability of a sequence of words is described with the help of the chain rule of probability, as shown above.
In the above equation, p is the prompt (the initial sequence of tokens provided to the model), and c is the completion (the response generated by the model). Therefore, for every prompt, the model generates a completion.
Support of the Distribution
To put it naively, the support of any probability distribution includes all the events in the sample space that have a non-zero probability.
Control System
A control system is a framework that represents the configuration of any dynamic system and regulates it to get the desired output. For our purposes, we can think of a control system as a black box that, given an input, gives us our desired output.
State Space and Reachability Set
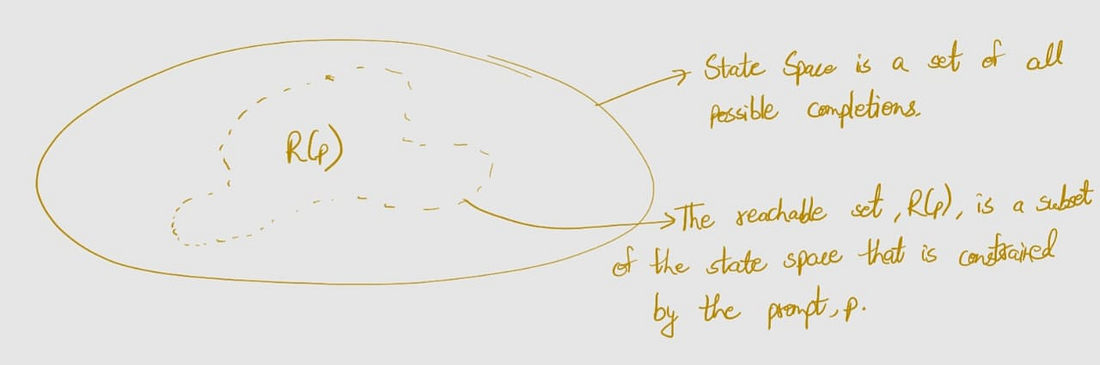
The state space is a discrete space encapsulating ALL possible configurations that a system can have.
The reachability set, on the other hand, is a subset of the state space and corresponds to the support of the distribution, i.e., includes all possible completions for any given prompt.
\[R(p) = {c|P(c|p) > 0}\]If you want to remember one thing from all the above definitions, remember this,
The reachability space is a subset of the state space that is constrained by the prompt provided to the language model. In other words, greater the cardinality of the reachability space, more probable it is that the output will be closer to the desired output.
How Do I Determine The Reachability Set For Any Prompt!?
Spoiler Alert — You don’t.
Okay, now we know that the state space is a very complex, high-dimensional space where each point represents a possible sequence.
THIS IS WHERE MANIFOLDS COME IN!
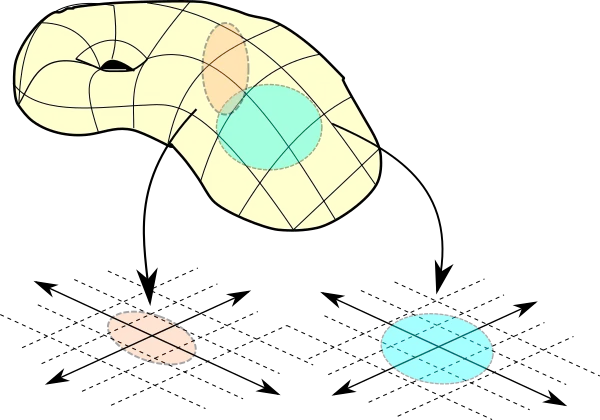
We want to create a manifold representation of the state space, i.e., a lower-dimensional representation where the high-dimensional input is mapped into a more compact form. In the field of machine learning, we call this the latent space. However, this space is popularly known as the embedding space in language modeling.
Whenever you are using a tokenizer and the tokenizer tells you that the word “dragon” has the input_id of 456 (say), what it is actually telling you is that I have a vocabulary where I will map “dragon” to the 456th embedding that I have already created in the n-dimensional space.
To approximate the reachability set, we can use multiple heuristic approaches like temperature sampling, beam search, nucleus sampling, etc., which are outside the scope of this article.
As mentioned earlier, we are interested in increasing the cardinality of the reachability set. Let us look at how CoT can help us achieve that.
Control System Framework For Language Models
Let us start by looking at the components of a language model,
State (x(t))
The hidden state or the internal representation of a language model at time step t encapsulates the context of the tokens generated so far.
Control Input (u(t))
The token generated by the model at the time step t.
Dynamics / Transition Map(f)
A non-linear function that updates the state of the system based on the control output.
To look at a more mathematical representation of the framework, we will borrow the definition of an LLM system with contorl input from the revolutionary paper “What’s the Magic Word? A Control Theory of LLM Prompting” by Bhargava A. et. al.
Alright! For those of you who didn’t quite get the essence of the definition above, the following statement should clear things up a bit,
In a sequence of length T, if an LLM is currently at a point x in the state space, then there will be a function (transition map) that will take the LLM to a new point x+1 based on the current token u.
Okay, all this sounds cool, but how does CoT help me guide my model?
We must first understand CoT as a high-level concept,
Chain-of-Thought (CoT) prompting generates intermediate steps to get to the final answer, rather than jumping directly to the conclusion.
Let us now look at the conditional probability for CoT prompting,
\[P_{\text{CoT}}(t_{1}, t_{2}, ..., t_{n}, a) = P(t_{1}|p).P(t_{1}|p, t_{1}).....P(t_{1}|p, t_{1}, t_{2}, ..., t_{n})\]From this, we can easily see that,
Each t introducecs new branching probabilites for subsequent steps, leading to a combinatorial expansion of the search space.
Each t represents a different path or reasoning strategy, which collectively cover a wider range of the state space.
This results in the following representation of a reachability set in the case of CoT prompting,
\[R_{\text{CoT}}(p) = \{x_{T}|x_{T}=\phi(x_{t}, u_{t}), u=(t_{1}, t_{2}, ..., t_{n}, a)\}\]or,
\[R_{\text{CoT}}(p) = \{x_{T}|x_{T}=\phi(\phi(...\phi(\phi(p), t_{1}), t_{2})..., a)\}\]I will give you a naive way of thinking about this geometrically (don’t quote me on this thought :)
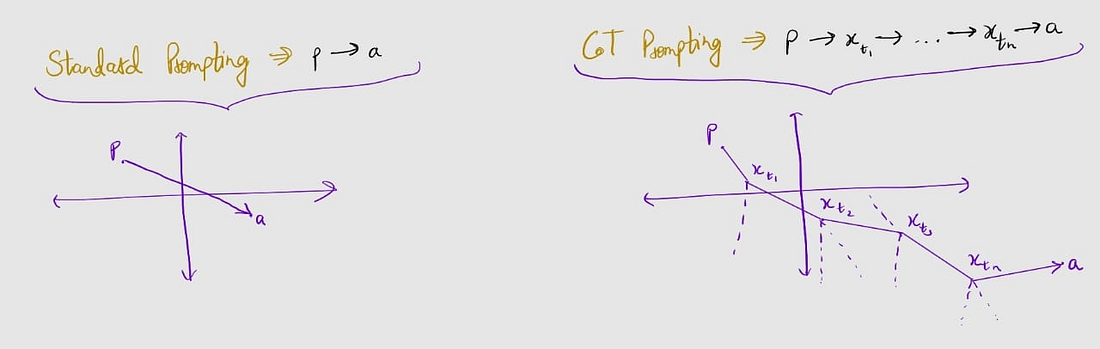
Therefore, we establish that with the help of CoT prompting, we can help our model explore more of the state space and give more accurate answers.
Before you close this article to go and watch Star Wars for the 5739th time, let me leave you with a few more questions to answer on your own,
1 — Can I get a theoretical proof about whether or not CoT prompting helps in avoiding the local minima on the manifold?
2 — If I now have a framework to define my LLM as a control system, can I make use of this knowledge to guide the models in uncharted territories? (One of the key tasks in the field of adversarial machine learning)
3 — Can there be a look-ahead mechanism in my model so that it can see if following a particular step will be beneficial or will it only increase latency? (This is somewhat abstract but is still a topic that fascinates me from time to time — for inspiration, you can read the “Lookahead Optimizer: k steps forward, 1 step back” paper by Zhang M. et al.)
REMEMBER — WHEN YOU START THINKING OF PROMPTS AS INITIAL GRADIENTS FOR YOUR OPTIMIZER, THEN ONLY YOU CAN START TO UNDERSTAND THE IMPORTANCE OF A GOOD PROMPT.
References
1 — Wei, J., Wang, X., Schuurmans, D., Bosma, M., Ichter, B., Xia, F., Chi, E., Le, Q., & Zhou, D. (2022). Chain-of-Thought Prompting Elicits Reasoning in Large Language Models. ArXiv. /abs/2201.11903
2 — Bhargava, A., Witkowski, C., Looi, S., & Thomson, M. (2023). What’s the Magic Word? A Control Theory of LLM Prompting. ArXiv. /abs/2310.04444